Hallo sobat matematika, pada blog ini kita akan membahas materi tentang integral tentu konsep luas. Apakah sobat matematika sudah tahu tentang integral tentu konsep luas??? Yuk, kita bahas bareng- bareng!!
Seperti halnya garis singgung yang mendasari turunan, masalah luas merupakan dasar
untuk pembahasan integral tentu khususnya luas poligon, baik poligon dalam maupun
poligon luar yang dapat dibuat pada bidang datar, didasarkan atas rumus luas persegi
panjang.
1. Luas Menurut Poligon Dalam
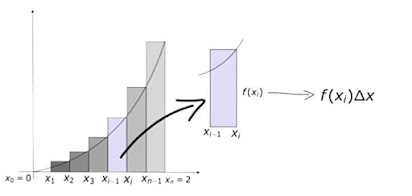
Sebagai contoh, akan dicari L(P) Luas Daerah datar yang dibatasi oleh kurva
y=f(x)= x
2
, sumbu –x, garis x = 0 dan x = 2. Pertama dipartisikan selang  atas selang bagian yang sama dengan panjang
atas selang bagian yang sama dengan panjang  , dan memakai titik-titik :
, dan memakai titik-titik :
Sehingga:
2. Luas Poligon Luar
Luas poligon luar :
Luas (Pluar) =
Sehingga:
Menurut teorema apit, maka untuk L(Pdalam)<L(P)<L(Pluar) didapat L(P)=8/3. Selanjutnya, diambil suatu fungsi f yang terdefinisi pada selang [a,b], partisikan selang [a,b] atas n selang bagian (tidak harus sama panjang) dengan memakai titik titik:
(jarak antara titik xi-1 dengan xi).
pada setiap selang bagian (xi-1, xi) dipilih titik sebarang ( boleh titik ujung), misalnya xi sebagai berikut:
Dari pembahasan di atas dengan memisalkan |P| menyatakan norma P, yaitu
panjang selang bagian terpanjang dari partisi P, maka dapat dibuat definisi sebagai
berikut:
Pada lambang
dx)
, a disebut batas bawah, dan b disebut batas atas dari
integral tersebut.
Dalam definisi dx)
, secara implisit kita menganggap bahwa a<b.
Menghilangkan batasan itu dengan definisi-defini berikut:
Nah itulah sobat matematika pembahasan materi mengenai integral tentu konsep luas, semoga sobat matematika bisa memahami materi ini dengan baik ...

.png)


.png)


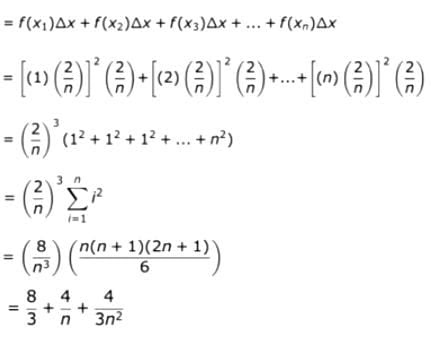











.jpeg)



